Najważniejsze informacje:
- System binarny używa tylko dwóch cyfr: 0 i 1.
- Każda pozycja w liczbie binarnej odpowiada potędze liczby 2.
- Aby przeliczyć liczbę binarną na dziesiętną, sumuj wartości potęg liczby 2 dla cyfr 1.
- Konwersja z dziesiętnego na binarny polega na dzieleniu przez 2 i zapisywaniu reszt.
- Ważne jest, aby unikać typowych błędów, takich jak niepoprawne sumowanie potęg lub błędne odczytywanie wyników.
Jak w prosty sposób liczyć w systemie binarnym i unikać błędów
System binarny to podstawowy sposób reprezentacji danych w informatyce, który opiera się na zrozumieniu tylko dwóch cyfr: 0 i 1. Każda z tych cyfr ma swoje miejsce w liczbie, a ich pozycja odpowiada potędze liczby 2. Dzięki temu, nawet skomplikowane obliczenia można przeprowadzać w prosty sposób, co czyni system binarny niezwykle istotnym w codziennym użytkowaniu komputerów oraz w programowaniu. W miarę jak zagłębiamy się w temat, zrozumienie podstaw systemu binarnego staje się kluczowe dla efektywnego posługiwania się nim. Właściwe zrozumienie zasad działania tego systemu pozwala na unikanie powszechnych błędów, które mogą prowadzić do nieprawidłowych wyników obliczeń. Wiedza ta jest niezbędna dla każdego, kto chce skutecznie operować danymi w świecie cyfrowym.Zrozumienie podstaw systemu binarnego dla łatwiejszych obliczeń
System binarny, znany także jako system dwójkowy, jest systemem liczbowym, który wykorzystuje tylko dwie cyfry: 0 i 1. W odróżnieniu od systemu dziesiętnego, który używa dziesięciu cyfr (od 0 do 9), system binarny operuje na podstawie potęg liczby 2. Każda cyfra w liczbie binarnej ma swoje miejsce, które odpowiada potędze liczby 2, zaczynając od prawej strony, gdzie znajduje się 2^0. Na przykład, w liczbie binarnej 1011, cyfra 1 na skrajnej lewej pozycji reprezentuje 2^3, co daje 8, a cyfra 1 na drugiej pozycji od lewej to 2^2, co daje 4.
Zrozumienie systemu binarnego jest kluczowe w informatyce, ponieważ większość nowoczesnych technologii opiera się na tym właśnie systemie. Komputery, procesory i różnorodne urządzenia elektroniczne działają na zasadzie przetwarzania danych w formie binarnej. Właściwe zrozumienie podstaw tego systemu umożliwia łatwiejsze wykonywanie obliczeń oraz programowanie, a także pozwala na lepsze zrozumienie działania technologii, z których korzystamy na co dzień. Dzięki temu, osoby pracujące w branży IT mogą efektywniej rozwiązywać problemy oraz unikać błędów, które mogą wyniknąć z nieznajomości zasad działania systemu binarnego.
Co to jest system binarny i jak działa?
System binarny to podstawowy system liczbowy, który wykorzystuje tylko dwie cyfry: 0 i 1. Każda cyfra w tym systemie ma swoje miejsce, które odpowiada potędze liczby 2. Na przykład, w liczbie binarnej 1011, pierwsza cyfra od prawej (1) reprezentuje 2^0, co daje 1, druga cyfra (1) to 2^1, co daje 2, a trzecia cyfra (0) nie wnosi nic do sumy. Ostatnia cyfra (1) to 2^3, co daje 8. W sumie, liczba 1011 w systemie binarnym odpowiada liczbie dziesiętnej 11 (8 + 2 + 1).
System binarny działa na zasadzie operacji logicznych, które są podstawą działania komputerów i innych urządzeń elektronicznych. Dzięki wykorzystaniu tylko dwóch cyfr, system binarny jest niezwykle efektywny w przechowywaniu i przetwarzaniu informacji. Komputery interpretują te cyfry jako stany elektryczne, co sprawia, że system binarny jest fundamentem nowoczesnej technologii.
Dlaczego warto znać system binarny w obliczeniach?
Znajomość systemu binarnego jest niezwykle ważna w dzisiejszym świecie technologii i informatyki. Wiele urządzeń, takich jak komputery, smartfony czy serwery, opiera swoje działanie na systemie binarnym. Zrozumienie, jak ten system funkcjonuje, pozwala na lepsze zrozumienie działania oprogramowania, a także umożliwia efektywne programowanie i tworzenie algorytmów. Wiedza ta jest kluczowa dla programistów, inżynierów oraz wszystkich, którzy pracują z danymi cyfrowymi.
Dodatkowo, umiejętność przeliczania liczb między systemami binarnym a dziesiętnym jest przydatna w wielu dziedzinach, takich jak informatyka, elektronika czy matematyka. Osoby zrozumiejące zasady działania systemu binarnego mogą lepiej analizować i rozwiązywać problemy związane z obliczeniami, co znacząco podnosi ich wartość na rynku pracy.
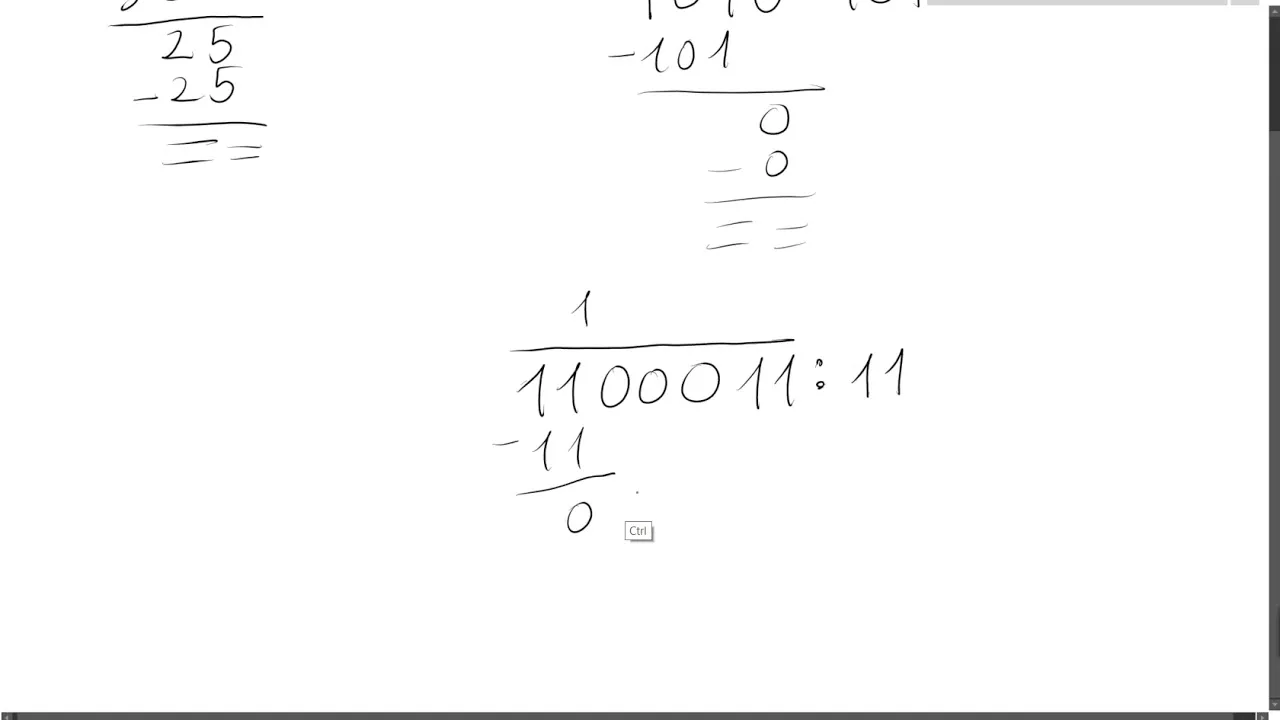
Jak przeliczać liczby binarne na dziesiętne krok po kroku
Aby przeliczyć liczby binarne na dziesiętne, należy zastosować metodę sumowania potęg liczby 2. Każda cyfra w liczbie binarnej ma swoje miejsce, które odpowiada potędze liczby 2, zaczynając od prawej strony. Na przykład, w liczbie binarnej 1011, pierwsza cyfra (1) to 2^0, druga cyfra (1) to 2^1, trzecia cyfra (0) to 2^2, a czwarta cyfra (1) to 2^3. Aby uzyskać wartość dziesiętną, należy zsumować wartości potęg dla każdej pozycji, w której znajduje się cyfra 1. W ten sposób, liczba binarna 1011 przelicza się na 8 + 2 + 1, co daje 11 w systemie dziesiętnym.
Teraz, przyjrzyjmy się kilku przykładom konwersji liczby binarnej na dziesiętną. Użyjemy tej samej metody, sumując wartości potęg dla cyfr 1 w różnych liczbach binarnych. Na przykład, liczba binarna 1101 przelicza się na 8 + 4 + 0 + 1, co daje 13. Innym przykładem może być liczba 1010, która przelicza się na 8 + 0 + 2 + 0, co daje 10. Dzięki tej metodzie, przeliczanie liczb binarnych na dziesiętne staje się prostym i efektywnym procesem.
Przykłady konwersji z binarnego na dziesiętny
Aby lepiej zrozumieć proces konwersji liczb binarnych na dziesiętne, warto przyjrzeć się kilku konkretnym przykładom. Używając metody sumowania potęg liczby 2, możemy łatwo przeliczyć różne liczby binarne na ich odpowiedniki w systemie dziesiętnym. Na przykład, liczba binarna 1100 przelicza się na 8 + 4 + 0 + 0, co daje 12. Inny przykład to liczba 1111, która przelicza się na 8 + 4 + 2 + 1, co daje 15. Poniższa tabela przedstawia kilka kolejnych przykładów konwersji.
| Liczba binarna | Liczba dziesiętna |
|---|---|
| 1010 | 10 |
| 1001 | 9 |
| 0110 | 6 |
| 0011 | 3 |
Proces dzielenia przez 2 i zapisywania reszt
Aby przeliczyć liczbę dziesiętną na binarną, stosuje się metodę dzielenia przez 2 i zapisywania reszt z tych dzielen. Proces ten polega na wielokrotnym dzieleniu danej liczby przez 2, aż do momentu, gdy wynik dzielenia osiągnie 0. Przy każdym dzieleniu zapisujemy resztę, która może wynosić 0 lub 1. Gdy mamy już wszystkie reszty, odczytujemy je w odwrotnej kolejności, co daje nam odpowiednik binarny liczby dziesiętnej. Ta metoda jest prosta i skuteczna, a jej zrozumienie jest kluczowe dla efektywnego konwertowania liczb w systemie binarnym.
Przykłady konwersji z dziesiętnego na binarny
Przyjrzyjmy się kilku przykładom konwersji liczb dziesiętnych na binarne za pomocą opisanego wcześniej procesu. Na przykład, liczba 10 dzielona przez 2 daje resztę 0, a następnie 5 dzielone przez 2 daje resztę 1, kontynuując ten proces, otrzymujemy binarną reprezentację. Kolejnym przykładem jest liczba 13, która po zastosowaniu tej samej metody daje wynik 1101. Poniższa tabela przedstawia kilka kolejnych przykładów konwersji.
| Liczba dziesiętna | Liczba binarna |
|---|---|
| 5 | 101 |
| 7 | 111 |
| 12 | 1100 |
| 15 | 1111 |
Jak wykorzystać system binarny w programowaniu i technologii
Znajomość systemu binarnego ma kluczowe znaczenie nie tylko w konwersji liczb, ale także w programowaniu i technologii informacyjnej. Wiele języków programowania, takich jak C, Python czy Java, wykorzystuje system binarny do reprezentacji danych. Na przykład, w programowaniu niskopoziomowym, zrozumienie, jak działa system binarny, pozwala na efektywne zarządzanie pamięcią oraz optymalizację algorytmów. Programiści często używają operacji bitowych, takich jak AND, OR i XOR, które są bezpośrednio oparte na zasadach działania systemu binarnego, co umożliwia bardziej wydajne przetwarzanie danych.
W przyszłości, wraz z rozwojem technologii komputerowych i sztucznej inteligencji, umiejętność pracy z systemem binarnym stanie się jeszcze bardziej istotna. W kontekście uczenia maszynowego i analizy danych, zrozumienie, jak dane są reprezentowane w systemie binarnym, może pomóc w tworzeniu bardziej zaawansowanych modeli i algorytmów. Warto również zwrócić uwagę na rozwój technologii kwantowych, gdzie zasady działania opierają się na zupełnie innych koncepcjach, ale zrozumienie klasycznego systemu binarnego może stanowić solidną podstawę do nauki o nowych technologiach.

