Konwersja liczb dziesiętnych na system binarny może wydawać się skomplikowana, ale w rzeczywistości jest to prosty proces. Aby przeliczyć liczbę 3 na system binarny, wystarczy podzielić ją przez 2 i zapisać reszty w odpowiedniej kolejności. Dzięki temu zrozumienie, jak działa system binarny, staje się łatwiejsze i bardziej przystępne. W tym artykule szczegółowo przedstawimy, jak dokonać konwersji liczby 3 na postać binarną. Omówimy także, dlaczego znajomość systemu binarnego jest ważna oraz jakie ma zastosowania w informatyce. Dzięki temu każdy, niezależnie od poziomu zaawansowania, będzie mógł zrozumieć ten kluczowy temat.
Najważniejsze informacje:
- System binarny używa tylko dwóch cyfr: 0 i 1.
- Liczba 3 w systemie binarnym to 11, co oznacza 21 + 20.
- Aby przeliczyć liczbę dziesiętną na binarną, dzielimy ją przez 2 i zapisujemy reszty.
- Każda reszta odzwierciedla wartość bitu w systemie binarnym.
- Znajomość konwersji liczb dziesiętnych na binarne jest istotna w programowaniu i informatyce.
Jak przeliczyć liczbę 3 na system binarny – prosty proces konwersji
W systemie binarnym liczba 3 jest zapisywana jako 11. System binarny to sposób reprezentacji liczb, który używa jedynie dwóch cyfr: 0 i 1. W przeciwieństwie do systemu dziesiętnego, który jest oparty na dziesięciu cyfrach (0-9), system binarny jest podstawą dla wszystkich nowoczesnych technologii komputerowych. Zrozumienie tego systemu jest kluczowe dla programowania i informatyki, ponieważ wszystkie operacje w komputerach odbywają się w języku binarnym.
Aby przeliczyć liczbę 3 na system binarny, należy wykonać kilka prostych kroków. Po pierwsze, dzielimy 3 przez 2. Wynik to 1, a reszta to 1. Następnie dzielimy 1 przez 2, co daje wynik 0 i resztę 1. Zapisując reszty w odwrotnej kolejności, otrzymujemy liczbę binarną 11. Wartości bitów w tej liczbie odpowiadają potęgom liczby 2: 1 * 21 + 1 * 20 = 2 + 1 = 3. Dzięki tym prostym krokom można łatwo zrozumieć, jak wygląda konwersja liczby 3 do systemu binarnego.
Zrozumienie systemu binarnego i jego podstawowych zasad
System binarny jest kluczowym elementem w świecie technologii i informatyki. Opiera się na dwóch podstawowych cyfrach: 0 i 1. Każda cyfra w tym systemie nazywana jest bitem, a osiem bitów tworzy bajt. Wszystkie dane w komputerach, od tekstu po obrazy, są reprezentowane w postaci binarnej. System binarny jest prostszy do zrozumienia dla maszyn, ponieważ działa na zasadzie włączania i wyłączania, co odpowiada wartościom 1 i 0. Z tego powodu, znajomość zasad działania systemu binarnego jest niezbędna dla każdego, kto chce zrozumieć, jak działają komputery i technologie informatyczne.
Krok po kroku: konwersja liczby 3 na system binarny
Aby przeliczyć liczbę 3 na system binarny, należy wykonać kilka prostych kroków. Proces ten polega na dzieleniu liczby przez 2 i zapisywaniu reszt. Zaczynamy od podzielenia 3 przez 2. Wynik dzielenia to 1, a reszta to 1. Następnie dzielimy 1 przez 2, co daje nam wynik 0 i resztę 1. Gdy mamy już wszystkie reszty, zapisujemy je w odwrotnej kolejności, co daje nam liczbę binarną 11. Ostatecznie, liczba 3 w systemie binarnym to 11.
- Podziel 3 przez 2, otrzymując wynik 1 i resztę 1.
- Podziel 1 przez 2, otrzymując wynik 0 i resztę 1.
- Zapisz reszty w odwrotnej kolejności, co daje 11.
Dlaczego warto znać konwersję liczby dziesiętnej na binarną?
Znajomość konwersji liczby dziesiętnej na binarną ma wiele praktycznych zastosowań. W dzisiejszym świecie, w którym technologia odgrywa kluczową rolę, umiejętność rozumienia i stosowania systemu binarnego jest niezbędna w wielu dziedzinach, takich jak programowanie, inżynieria komputerowa czy analiza danych. Wiele urządzeń elektronicznych, takich jak komputery i telefony, działa w oparciu o system binarny, co sprawia, że jego znajomość jest niezwykle ważna.Oprócz zastosowań praktycznych, nauka konwersji liczb dziesiętnych na binarne rozwija umiejętności analityczne i logiczne. Dzięki temu można lepiej zrozumieć, jak działają algorytmy oraz jakie są podstawy programowania. Ułatwia to również naukę bardziej zaawansowanych tematów w informatyce, takich jak struktury danych czy algorytmy sortowania. Warto więc zainwestować czas w naukę konwersji, ponieważ przynosi to długofalowe korzyści w karierze zawodowej.
Praktyczne zastosowania systemu binarnego w informatyce
System binarny ma kluczowe znaczenie w informatyce i technologii. Przede wszystkim jest on podstawą reprezentacji danych w komputerach. Wszystkie informacje, takie jak tekst, obrazy czy dźwięki, są konwertowane na postać binarną, co pozwala na ich przechowywanie i przetwarzanie. Na przykład, w programowaniu, zmienne i instrukcje są kodowane w systemie binarnym, co umożliwia komputerom wykonywanie złożonych operacji. Dodatkowo, system binarny jest stosowany w algorytmach kompresji danych, co pozwala na efektywne zarządzanie przestrzenią dyskową.
Innym ważnym zastosowaniem systemu binarnego jest jego rola w komunikacji sieciowej. Protokół TCP/IP, który jest podstawą działania Internetu, wykorzystuje binarną reprezentację danych do przesyłania informacji między urządzeniami. Dzięki temu, niezależnie od rodzaju przesyłanych danych, system binarny zapewnia ich integralność i poprawność. Wreszcie, system binarny jest również istotny w kryptografii, gdzie wykorzystywany jest do szyfrowania i deszyfrowania informacji, co zapewnia bezpieczeństwo danych w sieci.
Korzyści z nauki konwersji liczby w różnych kontekstach
Nauka konwersji liczb dziesiętnych na binarne przynosi wiele korzyści w różnych dziedzinach. Przede wszystkim rozwija umiejętności analityczne i logiczne, które są niezbędne w programowaniu oraz inżynierii komputerowej. Osoby, które potrafią przeliczyć liczbę 3 na system binarny, lepiej rozumieją działanie algorytmów oraz struktur danych, co ułatwia naukę bardziej zaawansowanych tematów. Dodatkowo, umiejętność ta jest cenna na rynku pracy, ponieważ wiele stanowisk w branży IT wymaga znajomości systemów liczbowych.
Regularne ćwiczenie konwersji liczb binarnych może znacznie poprawić zrozumienie zagadnień związanych z technologią. Praktyka w tej dziedzinie nie tylko zwiększa pewność siebie, ale także otwiera drzwi do kariery w programowaniu, analizie danych czy bezpieczeństwie informacji. Dlatego warto poświęcić czas na naukę i doskonalenie umiejętności związanych z systemem binarnym.
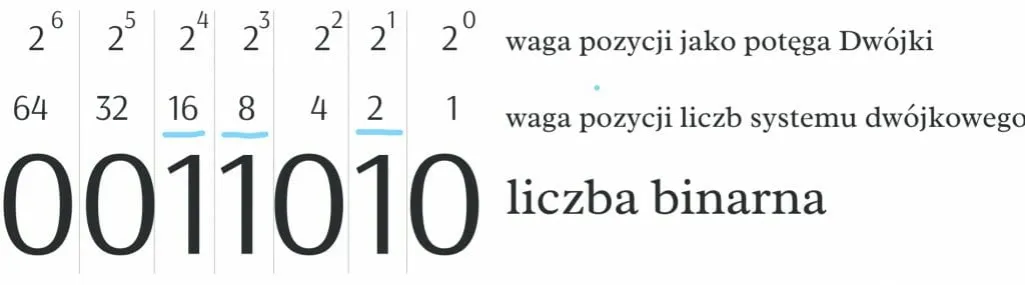
Inne przykłady konwersji liczb dziesiętnych na binarne
Konwersja liczb dziesiętnych na system binarny jest procesem, który można zastosować do wielu różnych wartości. Poniżej przedstawiamy kilka przykładów konwersji, aby zobrazować, jak różne liczby dziesiętne są reprezentowane w systemie binarnym. Na przykład, liczba 5 w systemie binarnym to 101, liczba 10 to 1010, a liczba 15 to 1111. Każda z tych konwersji pokazuje, jak liczby dziesiętne przechodzą do postaci binarnej, co może być przydatne w różnych kontekstach informatycznych.
Obserwując te konwersje, można zauważyć pewne wzorce. Na przykład, liczby parzyste zawsze kończą się na 0 w systemie binarnym, podczas gdy liczby nieparzyste kończą się na 1. Dodatkowo, każda kolejna potęga liczby 2 dodaje dodatkowy bit do reprezentacji binarnej. Dzięki tym wzorcom można łatwiej zrozumieć, jak działają konwersje i przewidywać, jak będą wyglądały inne liczby w systemie binarnym.
| Liczba dziesiętna | Liczba binarna |
|---|---|
| 3 | 11 |
| 5 | 101 |
| 10 | 1010 |
| 15 | 1111 |
| 20 | 10100 |
Jak przeliczyć inne liczby na system binarny – przykłady
Konwersja różnych liczb dziesiętnych na system binarny jest prostym procesem, który można zastosować do wielu wartości. Na przykład, liczba 5 w systemie binarnym to 101, co uzyskuje się poprzez podział przez 2: 5 dzielone przez 2 daje 2 z resztą 1, a następnie 2 dzielone przez 2 daje 1 z resztą 0. Kolejnym przykładem jest liczba 10, która w systemie binarnym zapisywana jest jako 1010. Proces konwersji polega na dzieleniu liczby przez 2 i zapisywaniu reszt, co prowadzi do uzyskania liczby binarnej. Liczba 15 to 1111, co również można uzyskać poprzez podobne dzielenie, zapisując reszty w odwrotnej kolejności.
Różnice w konwersji liczb parzystych i nieparzystych
Podczas konwersji liczb dziesiętnych na system binarny istnieją wyraźne różnice między liczbami parzystymi a nieparzystymi. Liczby parzyste zawsze kończą się na 0 w systemie binarnym, co oznacza, że ostatni bit to 0. Na przykład, liczba 4 w systemie binarnym to 100, a liczba 8 to 1000. Z kolei liczby nieparzyste kończą się na 1, co można zaobserwować w przypadku liczby 3 (11) oraz 5 (101). Ta zasada jest przydatna, ponieważ pozwala szybko określić, czy dana liczba jest parzysta czy nieparzysta, patrząc na jej reprezentację binarną.
Jak zastosować system binarny w programowaniu i technologii
Znajomość systemu binarnego nie tylko ułatwia konwersję liczb dziesiętnych, ale także otwiera drzwi do zaawansowanych technik programowania i rozwoju oprogramowania. Wiele języków programowania, takich jak C++, Python czy Java, wykorzystuje system binarny do reprezentacji danych, co jest kluczowe w procesach takich jak kompresja plików, szyfrowanie danych oraz optymalizacja algorytmów. Zrozumienie, jak liczby binarne wpływają na wydajność kodu, może pomóc programistom w pisaniu bardziej efektywnych i wydajnych aplikacji.
W przyszłości, z rozwojem technologii takich jak sztuczna inteligencja i uczenie maszynowe, zrozumienie systemu binarnego stanie się jeszcze ważniejsze. Algorytmy AI często operują na dużych zbiorach danych, które muszą być przetwarzane w sposób efektywny. Wykorzystanie technik binarnych do reprezentacji i przetwarzania danych pozwoli na szybsze i bardziej efektywne działanie modeli. Dlatego warto inwestować czas w naukę i praktykowanie konwersji oraz zastosowań systemu binarnego, aby być na bieżąco z nadchodzącymi trendami w technologii.

